Bio

I am associate professor at UiT, The Arctic University of Norway, Tromsø, the northernmost university in the world. I was previously researcher at EPFL, Lausanne Switzerland. My research is now focused on Machine Learning, but I have been doing research in different fields: Data Science, Network Science, Signal Processing and Physics. I am a member of the machine learning group at UiT. I have a background in mathematical physics and my PhD (a long time ago!) was on Quantum Mechanics.

A few more details about myself:

• I am the co-director of the Center of Excellence Integreat which is the Norwegian Centre for Knowledge-driven Machine Learning,
• I am co-founder and member of the Northernmost GraphML Group,
• I am teaching Image Analysis, Machine Learning and Generative AI at UiT.
• I am program chair for the Northern Light Deep Learning conference that takes place every year in January in Tromsø,
• I develop, with my students, some cool outreach activities about AI for kids and the general public: we have made open-source machine learning and AI demos for the Science Centre in Tromsø. Our lastest very fun demo is the AI Photobooth.

A short description of my main research topics:

• Machine Learning and AI
• Graph signal processing
• Methods for exploring large graphs (web and social networks)
• Graphs in biology
• Machine learning in audio and explainable AI
• Sparsity in data and models

Machine Learning and AI

Machine Learning is evolving very fast and there are many interesting and exiting directions at the moment.

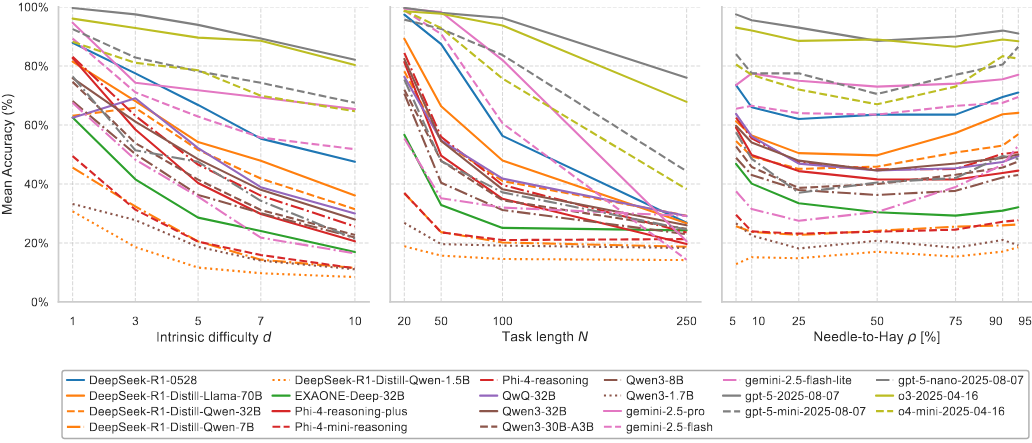Reasoning in Large Language Models. We have made a benchmark for evaluating the reasoning abilities of Large Language Models [Kai25]. It consists on text puzzles that the model has to solve. Our novelty is that the puzzles are generated automatically, preventing training on them and memorization. In addition, it tests 3 different difficulty dimensions, related to cognitive load theory. It is written in simple text to be sure the models are all able to follow the steps, and focus only on the deduction ability of models.

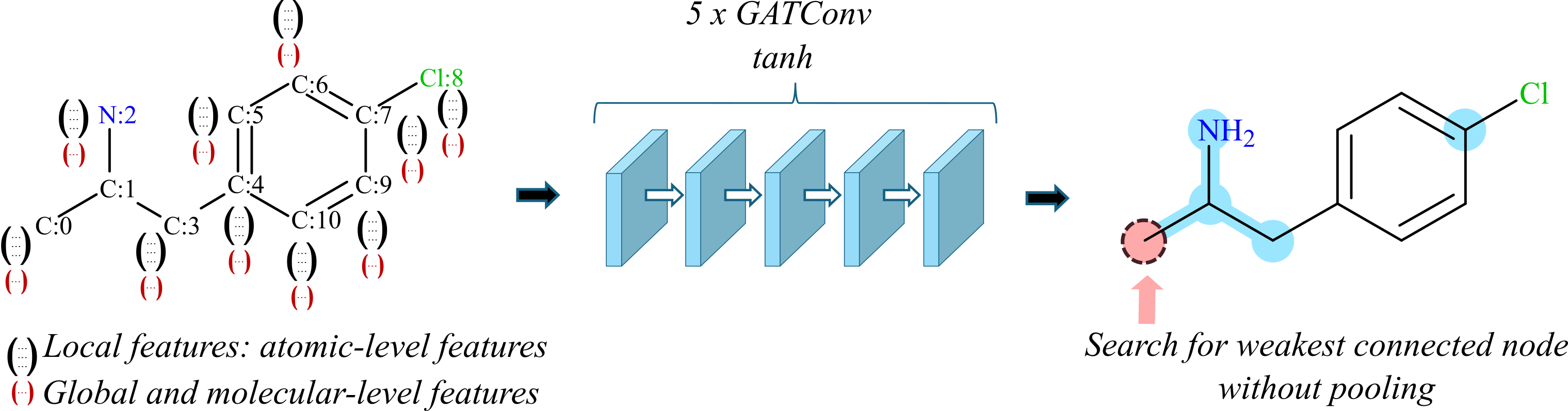Graph Machine Learning for molecules. Molecules can be seen as graphs, with atoms as nodes and chemical bonds as edges. Graph neural networks are very efficient for the classification and prediction of molecule properties. We show that combining a graph approach with apriori knowledge from chemistry (using molecular fingerprints) gives the best results for predicting particular molecule properties [Lut25].

Self-supervised learning for applications. Many applications have data with few or no labels, and standard supervised learning is impossible. We have developed a self-supervised model, a “foundation model”, for microfossil classification [Mar24]. This model frees geologists from manual counting and classification of microfossils and hence is a great contribution to their field. In another project, together with physicists, we have made a self-supervised model to denoise and classify spectra collected from a Raman spectrometer. The model’s latent representation turn out to be very useful for classifying biological vesicles [Jen24].

[Kai25] D Kaiser, A Frigessi, A Ramezani-Kebrya, B Ricaud, CogniLoad: A Synthetic Natural Language Reasoning Benchmark With Tunable Length, Intrinsic Difficulty, and Distractor Density, arXiv preprint arXiv:2509.18458, 2025 [Lut25] T Lutchyn, M Mardal, B Ricaud, Efficient learning of molecular properties using Graph Neural Networks enhanced with chemistry knowledge, ACS omega, 2025 [Mar24] Martinsen, Iver and Wade, David and Ricaud, Benjamin and Godtliebsen, Fred, The 3-Billion Fossil Question: How to Automate Classification of Microfossils, Artificial Intelligence in Geosciences, Volume 5, 2024.
[Jen24] Jensen M.N., Guerreiro E.M., Enciso-Martinez A., Kruglik, S.G., Otto C., Snir O., Ricaud B., Hellesø O.G., Identification of extracellular vesicles from their Raman spectra via self-supervised learning. Nature Sci Rep 14, 6791 (2024).

Graph signal processing

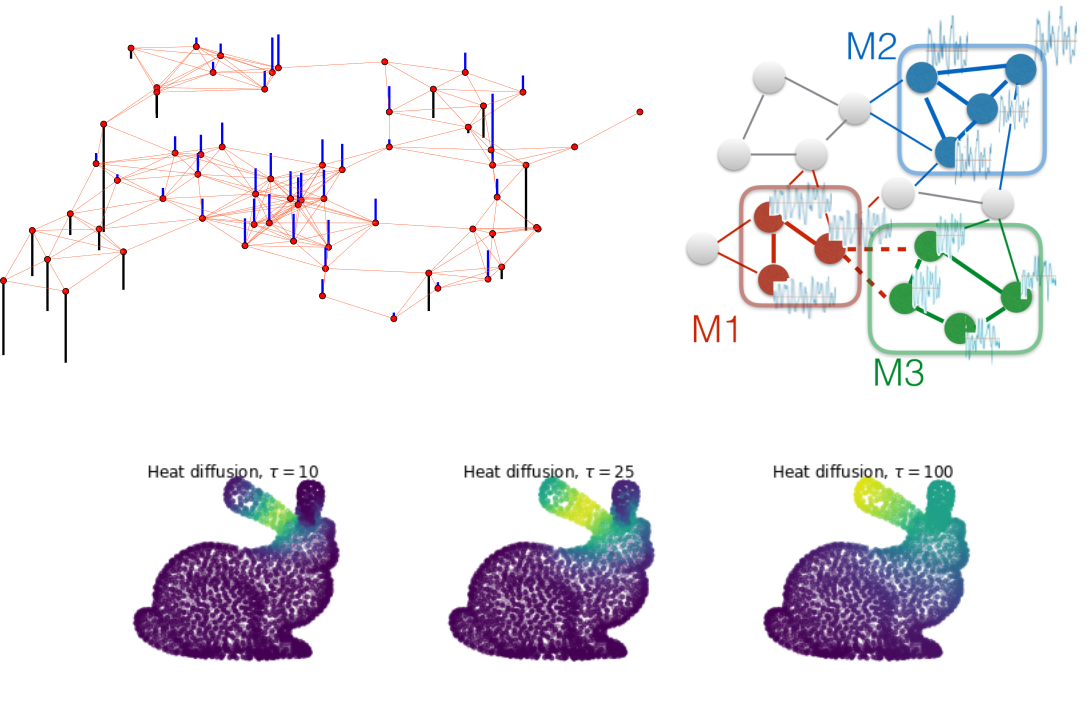Since I joined the LTS2 lab at EPFL in 2012, I have been working on graph structured data. The main idea is to design new methods enabling the analysis of phenomena occurring within networks. With the explosion of data, these structures arise in many different fields of application (engineering, biology, physics…). In graph signal processing and graph machine learning, we distinguish two sources of information we combine together: 1) the graph and 2) the data associated to the graph nodes or edges. The graph is the structure or space and the data are the signal or feature vectors. Our first effort was to show how standard data analysis methods in 1D or 2D could be generalized to this exotic graph space. We have generalized key signal processing methods and concepts to the graph setting such as the Fourier transform, the concept of frequency and sparse representation [GSP1], the windowed Fourier transform [GSP2], dynamic analysis on graphs [GSP3] and the concept of uncertainty [GSP4]. With some co-authors and friends, we wrote a review paper about these methods [GSP5].

[GSP1] David I Shuman, Benjamin Ricaud, and Pierre Vandergheynst. A windowed graph fourier transform. In Statistical Signal Processing Workshop (SSP), 2012 IEEE, pages 133–136. Ieee, 2012.
[GSP2] Shuman, D. I., Ricaud, B., & Vandergheynst, P. (2016). Vertex-frequency analysis on graphs. Applied and Computational Harmonic Analysis, 40(2), 260-291.
[GSP3] Francesco Grassi, Andreas Loukas, Nathanael Perraudin, and Benjamin Ricaud. A time-vertex signal processing framework: Scalable processing and meaningful representations for time-series on graphs. IEEE Transactions on Signal Processing, 66(3):817–829, 2018.
[GSP4] PERRAUDIN, Nathanael, RICAUD, Benjamin, SHUMAN, David I., et al. Global and local uncertainty principles for signals on graphs. APSIPA Transactions on Signal and Information Processing, 2018, vol. 7.
[GSP5] Benjamin Ricaud, Pierre Borgnat, Nicolas Tremblay, Paulo Gonçalves, and Pierre Vandergheynst. Fourier could be a data scientist: From graph fourier transform to signal processing on graphs. Comptes Rendus Physique, 20(5):474 – 488, 2019.

Exploration of Large graphs

With the increasing size of networks, many methods based on matrix computations, in graph signal processing, or machine learning reach their limits. New approaches are needed, involving more scalable processes. We have developed several such approaches. One of them is the analysis of abnormal activity (or peak of activity) in the large network of Wikipedia hyperlinks. To this enormous network of articles and hyperlink (millions of nodes), we add the number of visits per hour for each page (open data provided by Wikimedia). Our method is able to focus on graph regions with an abnormal dynamic activity amid the overwhelming amount of data to treat. Besides the demonstration of scalability, we also get interesting insights on the human curiosity and behavior related to important events and news [W1,W2,W3]. A presentation of the findings is available on a blog post of my co-author V. Miz. In a second aplication, we establish efficient exploration methods for social networks, emblematic examples of large scale networks. I was involved in a project with the Swiss media consortium IMI to analyze and track controversies and fake news in social networks. In addition to the size of the network, the limited access to the social platform via an API is a challenge. We have proposed an innovative network exploration principle to unlock the exploration of social networks [SP4]. It is based on a random subsampling of the networks of users and retweets. This subsampling allow a fast and accurate detection of communities and information bubbles. We analysed its efficiency together with journalists in [Car21].

[W1] Miz, V., Ricaud, B., Benzi, K., & Vandergheynst, P. (2019, May). Anomaly detection in the dynamics of web and social networks using associative memory. In The World Wide Web Conference (pp. 1290-1299).
[W2] Aspert, N., Miz, V., Ricaud, B., & Vandergheynst, P. (2019, May). A graph-structured dataset for Wikipedia research. In Companion Proceedings of The 2019 World Wide Web Conference (pp. 1188-1193).
[W3] Miz, V., Hanna, J., Aspert, N., Ricaud, B., & Vandergheynst, P. (2020, April). What is Trending on Wikipedia? Capturing Trends and Language Biases Across Wikipedia Editions. In Companion Proceedings of the Web Conference 2020 (pp. 794-801).
[SP4] Benjamin Ricaud, Nicolas Aspert, and Volodymyr Miz. Spikyball sampling: Exploring large networks via an inhomogeneous filtered diffusion. Algorithms, 13(11):275, 2020.
[Car21] Carlino, V., Pignard-Cheynel, N., Loubère, L., Ricaud, B., & Aspert N. (2021). Navigating digital trails on Twitter. A look back at the design of a data mapping system for journalists. Digital Intelligibility Review, 2, 2021.

Graphs in biology

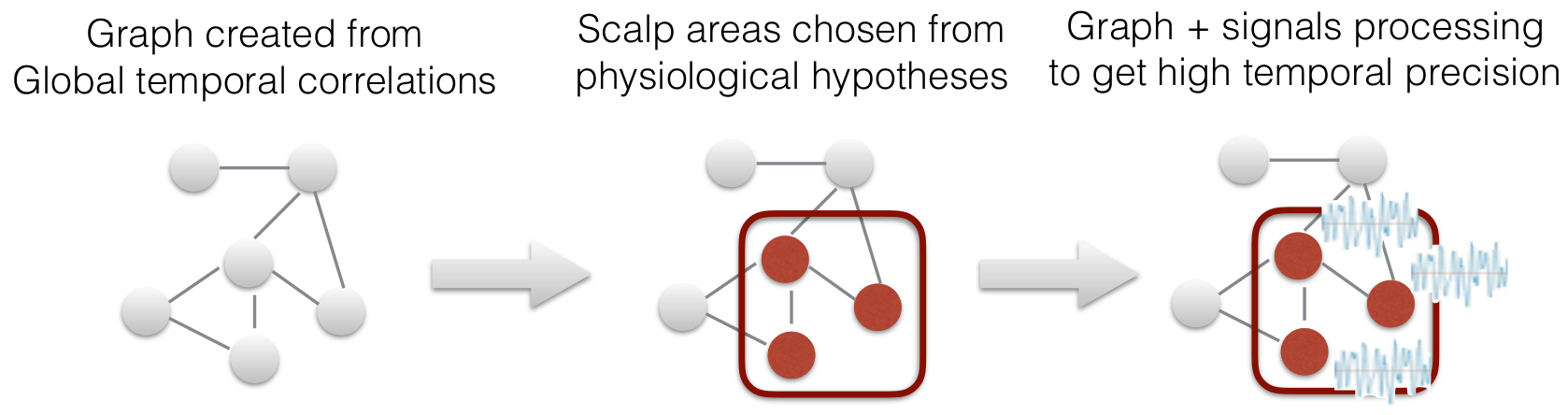I have worked on medical applications of graph signal processing, to understand the dynamical processes inside the brain (and its network of interconnected brain regions). In [BIO2] the network was the network of EEG sensors where their signals evolve over time as the patients are asked to complete a task. We showed that combining the temporal signals with a sensor network structure could reveal hidden correlations and help distinguish signs of early Alzheimer desease. In [BIO1] the combination of the graph of connected brain regions with the dynamic activity of these regions recorded from MRI scans improved the extraction of activity patterns such as the resting state network and revealed new patterns.

[BIO1] Alessandra Griffa, Benjamin Ricaud, Kirell Benzi, Xavier Bresson, Alessandro Daducci, Pierre Vandergheynst, Jean-Philippe Thiran, and Patric Hagmann. Transient networks of spatio-temporal connectivity map communication pathways in brain functional systems. NeuroImage, 155:490–502, 2017.
[BIO2] Keith Smith, Benjamin Ricaud, Nauman Shahid, Stephen Rhodes, John M Starr, Augustin Ibáñez, Mario A Parra, Javier Escudero, and Pierre Vandergheynst. Locating temporal functional dynamics of visual short-term memory binding using graph modular dirichlet energy. Nature Scientific Reports, 7:42013, 2017.

Machine learning in audio and explainable AI

I used to work on audio applications before coming to EPFL, as an application of more theoretical signal processing concepts. I studied sparse representation of audio and acoustic signals (time-frequency analysis). I recently came back to this topic with machine learning approaches combining signal processing. In a recent work, we have designed learnable filter banks inside a neural net layer [ML2]. These are convolutional layers with parameterized kernels, where the parameters are the cut-off frequencies and shape of band pass filters. The advantages are that these kernels can be interpreted and the learning is faster as there a less weights to learn. From a different perspective, in a collaboration with Logitech, we investigate state-of-the-art AI in audio signal processing (speech and music) and focus on reducing the size of the deep networks in order to make them faster to train, more convenient for real-world audio applications and possibly more explainable [ML1,ML3].

[ML1] Berkay Inan, Milos Cernak, Helmut Grabner, Helena Peic Tukuljac, Rodrigo CG Pena, and Benjamin Ricaud. Evaluating audiovisual source separation in the context of video conferencing. In INTER-SPEECH 2019, pages 4579–4583. ISCA, 2019.
[ML2] Helena Peic Tukuljac, Sparse and Parametric Modeling with Applications to Acoustics and Audio, Phd Thesis, EPFL, 2020. Article accepted: Helena Peic Tukuljac, Benjamin Ricaud, Nicolas Aspert, Laurent Colbois, Learnable filter-banks for CNN-based audio applications and their performances. Proceedings of the NLDL2022 conference.
[ML3] Alexandru Mocanu, Benjamin Ricaud, Milos Cernak, Fast accuracy estimation of deep learning based multi-class musical source separation, Proceedings of the NLDL2022 conference, 2022.

Sparsity in data

Prior to my work on graph signal processing and machine learning, I have worked on theoretical concepts in signal processing and graph signal processing such as sparsity and sparse signal representations [SP1, SP2, SP3]. These concepts are very general and appear in mathematics, physics and data science. The idea is to find representations of signals or data where the information is encoded in a sparse manner. “Summarizing” data with a smaller number of values is a key to compression as well as a to a clearer extraction, understanding and interpretability of the information within the data. This related to my background in Quantum Physics through the uncertainty principle.

[SP1] Benjamin Ricaud and Bruno Torrésani. Refined support and entropic uncertainty inequalities. IEEE Transactions on Information Theory, 59(7):4272–4279, 2013.
[SP2] Benjamin Ricaud and Bruno Torrésani. A survey of uncertainty principles and some signal processing applications. Advances in Computational Mathematics, 40(3):629–650, 2014.
[SP3] Benjamin Ricaud, David I Shuman, and Pierre Vandergheynst. On the sparsity of wavelet coefficients for signals on graphs. In Wavelets and Sparsity XV, volume 8858, page 88581L. International Society for Optics and Photonics, 2013.