For my english readers, this post is in French. It is talking about student data from the French education system so I thought it would be better to write it in French. Je suis récemment retourné au Lycée. Non pas comme élève mais comme professeur. Pendant 2 mois j’ai enseigné les mathématiques (ou du moins j’ai essayé!) et en regardant les notes des différents contrôles, je dois dire que j’étais un peu perplexe. En effet, la distribution des notes autour de la moyenne est singulière. Elle semble avoir parfois une forme gaussienne, plus ou moins étalée et d’autres fois une forme plus complexe avec, semble-t-il, une séparation en 2 groupes (2 Gaussiennes). Comme j’adore l’analyse de données et que j’ai tous les outils à ma disposition avec Python, j’ai plongé dans l’analyse des notes. J’ai utilisé non seulement des statistiques que je leur ai enseignés (au programme du Bac), mais c’était aussi l’occasion d’utiliser mes algorithmes favoris d’apprentissage automatique et intelligence artificielle, ici le modèle de mélange gaussien. Les résultats et l’analyse en elle-même sont intéressants et c’est pour ca que je les partage. Voilà ce que j’ai découvert…

Introduction

Comme mon entreprise a encore du mal à décoller, j’ai décidé de chercher des alternatives. Et récemment je suis tombé sur l’annonce d’un lycée qui cherchait un prof de math à mi-temps pour 2 mois. Ca me semblait parfait pour me changer un peu les idées et sortir du code informatique que je voyais toute la journée.

C’est une drôle d’expérience pour moi. Je dois avouer que je n’étais pas préparé à ca. J’ai appris beaucoup de choses durant ces 2 mois au contact des élèves. J’ai pu remarquer une première chose, les élèves n’ont pas le niveau de maturité auquel je m’attendais. Je les ai pris pour des adultes, je leur ai donné trop de liberté, et certains en ont profité. A la fin, bien sûr, cela se voit sur les notes.

J’ai enseigné les mathématiques aux élèves de la filière Bac Pro d’un lycée, donc les classes de seconde, première et terminale Bac Pro. Cette filière est particulière dans le sens où il y a une proportion plus grande d’élèves ayant des difficultés avec le système scolaire standard par rapport aux filières générales. Le Bac Pro est une voie plus rapide vers la fin des études et la vie active. Il y a aussi des élèves qui n’ont pas de difficulté particulière et qui ont fait le choix de cette filière par goût.

J’ai trouvé un niveau très hétérogène qui va des bons élèves sérieux et motivés jusqu’aux élèves en grande difficulté et totalement fermés aux mathématiques. Ces derniers ont toujours été en échec en mathématiques et ont baissé les bras, comme ils me l’ont dit en classe. Je me suis demandé comment ces personnes là évolueraient à l’approche du Bac. Prendraient-elles conscience de l’enjeu et se mettraient-elles au travail en classe de première ou de terminale? j’ai trouvé un début de réponse, en étudiant la distribution des notes de chaque classe.

Avertissement

L’analyse statistique porte sur 2 mois de cours et 3 classes de 30 élèves chacune. L’effectif est donc assez faible. Le lecteur ne doit rien conclure hâtivement car les résultats sur un si faible échantillon peuvent être simplement dus à des fluctuations statistiques.

But de l’analyse

On va étudier la distribution des notes des élèves autour de la moyenne. Ce que l’on s’attend à trouver, c’est une distribution gaussienne, la fameuse courbe en cloche que l’on voit sur la figure ci-dessous. On l’appelle encore “loi normale”.

Dans une telle configuration, beaucoup d’élèves se situent autour de la moyenne de la classe et plus les notes sont élevés plus le nombre d’élèves qui ont de telles notes diminue. De la même manière pour les mauvaises notes. Il faut imaginer que sur la figure, le centre de la courbe (le zéro) est en fait la note moyenne. Le symbole sigma est l’écart type et permet de caractériser l’étalement de la distribution autour de la moyenne. Si toutes les notes sont concentrées dans un petit intervalle autour de la moyenne, sigma aura une valeur faible. Pour les classes de Bac Pro, on va estimer ce sigma et vérifier aussi que l’on a bien une gaussienne.

Les Données

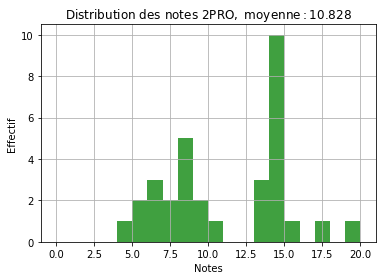
Pour les seconde Pro (2PRO), la moyenne de chaque élève a été obtenue avec 2 interrogations coefficient 2 et un devoir à la maison coefficient 1. J’ai été plutôt indulgent sur les notes et la moyenne de la classe est à 11.39. Ci-dessous, on peut voir la distribution des notes autour de la moyenne. L’histogramme montre le nombre d’élèves pour chaque note de 0 à 20. Par exemple, 2 élèves ont une note comprise entre 7 et 8 (les moins bonnes notes).

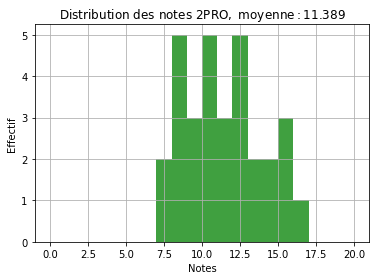
La distribution n’est pas une belle courbe en cloche et c’est normal. Quand on a peu de données (ici les notes de 30 élèves sur 3 interrogations), on a de fortes fluctuations statistiques. Un peu comme quand on fait des enfants, on a une chance sur 2 d’avoir une fille mais si on a 6 enfants, il est bien possible d’avoir 4, 5 voire même 6 filles. On a quand même, grossièrement, une allure de gaussienne, avec beaucoup d’élèves qui ont des notes autour de la moyenne de la classe, puis une diminution assez forte quand on s’en éloigne.

Pour les premières (1PRO), la moyenne a été calculée à partir de 2 interrogations. La moyenne est de 7.9. J’ai été plus sévère sur les notes mais je ne crois pas que ca ait eu un impact sur leur travail. Voici la distribution des notes.

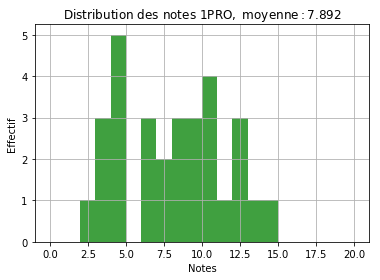
On remarque tout de suite que la distribution est plus étalée. Si on fait l’hypothèse que c’est une gaussienne, l’écart type est ici plus grand. Néanmoins, la distribution ne ressemble pas vraiment à une cloche. Il y aurait plutôt 2 bosses de part et d’autre de la moyenne, un peu comme s’il y avait 2 gaussiennes côte à côte. Ce pourrait être comme dans la figure ci-dessous (prise sur wikipedia):

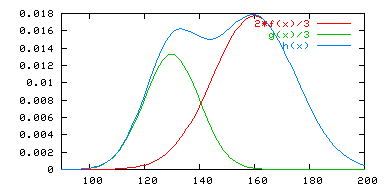
La courbe bleue est la somme des fonctions gaussiennes rouge et verte. Remarquez comme l’allure de cette courbe bleue ressemble à la distribution des notes, avec 2 “bosses” est un creux au milieu.

Voyons maintenant ce que donne la distribution pour les terminales (TPRO). On a ici seulement une interrogation.

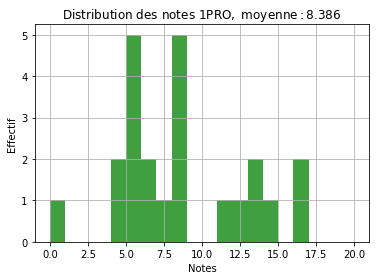
Le phénomène observé en 1PRO est ici encore plus criant. Il semble y avoir 2 groupes dans la classe: le groupe des bons élèves (entre 11 et 16) et le groupe des élèves qui ont décroché (majoritairement entre 4 et 8). On peut se demander d’abord si c’est une effet statistique et ensuite s’il s’agit d’une évolution des élèves vers 2 groupes distincts, au fur et à mesure des années de lycée. On va maintenant essayer de confirmer ou d’infirmer ce phénomène.

Estimation des distributions à l’aide d’apprentissage automatique

Pour trouver la courbe gaussienne la plus proche des données, il suffit de calculer la moyenne et l’écart-type des données (ces 2 fonctions sont disponible sur les calculatrices scientifiques, Excel ou bien en langage Python). On peut ainsi tracer la gaussienne paramétrée par ces 2 valeurs. Si les données sont issues d’une somme de plusieurs distributions gaussiennes, cela se complique un petit peu. Mais il existe des algorithmes pour résoudre ce problème, pourvu qu’on leur spécifie le nombre de gaussiennes à trouver. J’utilise ici le modèle de mélanges gaussiens. On doit faire l’hypothèse que les données sont issues de plusieurs groupes indépendants, suivant chacun une loi normale avec une moyenne et un écart type différent. Les informations à donner pour construire le modèle sont les notes et le nombre de groupes (le nombre de gaussiennes) que l’on suppose avoir dans la classe. Le programme va automatiquement donner les moyennes et écart types pour chaque groupe. les valeurs trouvées sont celles qui maximisent une quantité qui s’appelle la vraisemblance. L’algorithme en lui-même est intéressant mais je ne vais pas l’expliquer ici. Il mériterait un article de blog pour lui tout seul…

Ce modèle a bien sûr des limites. Il ne trouve pas forcement le maximum global de la vraisemblance et peut converger sur un maximum local. De plus, le nombre de notes reste faible pour faire une étude statistique et cela a une influence sur les résultats du modèle. Les algorithmes d’apprentissage automatiques ne font pas des miracles et restent tributaires de la qualité et la quantité des données.

En pratique, avec Python, on peut utiliser le module scikit-learn qui contient un ensemble assez complet de programmes d’apprentissage automatique (machine learning). On y trouve une version du modèle de mélanges gaussiens (Gaussian Mixture Model en anglais).

Détails d’implémentation

Ceci est une parenthèse sur l’utilisation de Python pour les calculs. Le lecteur qui n’est pas intéressé par le détail des calculs peut directement passer à la section “résultats”.

On importe le module scikit-learn et on lance la fonction comme suit:

from sklearn.mixture import GaussianMixture
n_groups=1
g = GaussianMixture(n_groups)
g.fit(notes)

où n_groups est le nombre de groupes que l’on suppose dans la classe et notes est la liste des notes sur une colonne. La commande g.fit va lancer l’algorithme et stocker les résultats dans différentes variables associées à g. Pour obtenir les résultats de chaque groupe, on peut utiliser la routine itérative suivante:

for group_id in range(n_groups):
    weight = g.weights_[group_id]
    mean = g.means_[group_id][0]
    sigma = np.sqrt(g.covariances_[group_id][0][0])
    print("GROUP",group_id)
    print("Weight",round(weight,2))
    print("Mean",round(mean,2))
    print("Sigma",round(sigma,2))

Ici, weight est le poids de chaque gaussienne, mean sa moyenne et sigma son écart type.

Résultats

Voici ce que l’on obtient pour les notes des 2PRO si on suppose un seul groupe:

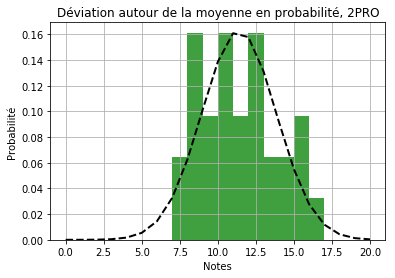
La gaussienne centrée en 11.39 et d’écart type 2.45 semble bien coller avec les données. Passons maintenant aux 1PRO. Supposons d’abord qu’il y a un seul groupe dans la classe. On obtient le résultat suivant.

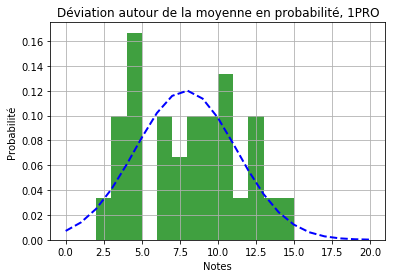
Si l’on suppose qu’il existe 2 groupes.

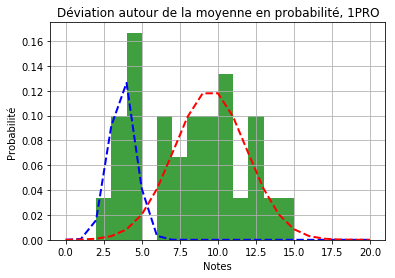
Il est difficile de départager ces résultats en regardant les graphiques. On va essayer de le faire plus objectivement, en utilisant le score “BIC” pour Bayesian Information Criterion ou critère d’information Bayésien. Selon ce critère, le modèle pour lequel la valeur BIC est la plus petite est le meilleur (le plus adapté à la distribution). La fonction Python utilisée ici (GaussianMixture) calcule pour nous cette valeur. Pour l’hypothèse avec 1 groupe cette valeur est 163.96 et pour 2 groupes elle est de 166.87.

Le modèle avec un seul groupe d’élèves décrit ici (légèrement) mieux notre distribution de notes. Remarquons que l’écart type de la gaussienne pour les 2PRO vaut 2.45 et pour les 1PRO, 3.32. On a donc une distribution des notes bien plus étalée pour les 1PRO, ce qu’on voit sur le graphique. Les différences entre bons élèves et élèves en difficulté sont plus accentués dans la classe de 1PRO, même si on ne peut pas parler de 2 groupes bien distincts.

Finissons par la classe de TPRO. J’ai écarté la note zéro d’une élève qui est sortie de l’interrogation sans me rendre sa copie. Je ne pense pas que cette note soit représentative et elle fausse la distribution, d’autant plus que les notes n’ont pas été moyennées sur plusieurs interrogations. Voici ce que l’on obtient avec l’hypothèse d’un groupe.

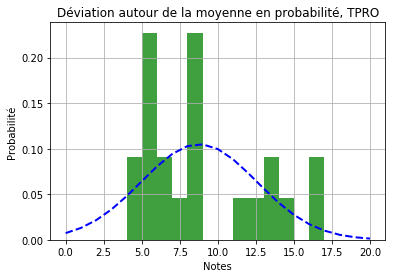
Il est plus difficile de voir la correspondance entre la distribution des notes et le modèle. Si l’on suppose qu’il existe 2 groupes:

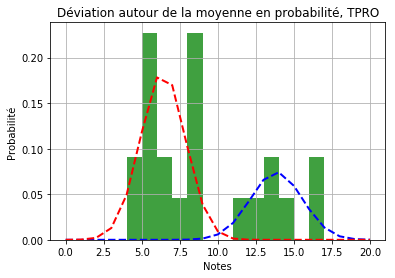
La représentation semble plus adaptée. Si l’on compare le BIC des 2 résultats, on a 127.37 pour le modèle à un groupe et 124.07 pour le modèle à 2 groupes. Il semble donc que le modèle à 2 groupes soit plus fidèle pour décrire la distribution des notes de TPRO. Cela confirme la tendance de séparation entre les élèves de la classe avec le groupe des “bons” et le groupe des élèves en difficulté qui ont baissé les bras.

Pour montrer les limites de cette étude, voici maintenant la distribution des notes pour une classe de Seconde générale, sur une interrogation courte de 30 minutes.

On voit ici aussi une séparation en 2 groupes, comme pour les TPRO. L’évolution en 2 groupes distincts en filière Bac Pro n’est finalement peut être pas une évolution mais juste le fait que la classe, pour cette interrogation, est divisée en 2. La manière dont les questions sont posées dans l’interrogation peut avoir eu une influence, dans le sens où soit on sait faire l’exercice et on a tous les points, soit on a aucun point. Ceci creuse l’écart entre les élèves qui ont compris et les autres. Il faudrait confirmer sur les prochaines interrogations.

Conclusion

Il faut rester prudent dans les conclusions avec une aussi faible quantité de données. Les résultats pourraient être dû purement au hasard mais je dois noter qu’ils sont en accord avec l’impression que j’ai eu en classe. En effet, j’ai trouvé la classe très hétérogène avec certains élèves attentifs et intéressés, qui posent des questions et d’autres totalement démotivés. Comme je le disais au début, certains élèves sont convaincus qu’ils ne sont pas bons en mathématiques et que ca ne sert à rien pour eux d’essayer de travailler.

Au delà de ces résultats, il reste donc le problème de gestion de la classe. Comment combiner de la meilleure manière ces différences de niveaux afin que les élèves en difficulté se motivent et suivent et que les bons élèves ne s’ennuient pas non plus (sinon, ce sont eux qui vont commencer à bavarder et à gêner le cours). Je n’ai pour le moment pas de solution pour cela.

Même s’il est difficile de conclure, c’est tout de même un bon exercice de math et d’apprentissage automatique. Un algorithme important du domaine (le modèle de mélanges gaussiens) est utilisé et on voit son application pratique, avec les conditions dans lesquelles on peut l’utiliser, comment l’appliquer et ses limites. On voit aussi un problème central dans l’analyse de données en statistiques et en intelligence artificielle : on a besoin d’un grand, voire très grand, nombre de données pour avoir un apprentissage de qualité, et pouvoir extraire de l’information pertinente de celles-ci.